[10000ダウンロード済み√] tan^2 identities 252178-Tan^2 identities

Instead, think that the tangent of an angle in the unit circle is the slope If you pick a point on the circle then the slope will be its y coordinate over its x coordinate, ie y/x So at point (1, 0) at 0° then the tan = y/x = 0/1 = 0 At 45° or pi/4, we are at an x, y of (√2/2, √2/2) and y / x for those weird numbers is 1 so tan 45As we know, from trigonometry identities, 1tan 2 A = sec 2 A sec 2 A – 1 = tan 2 A (1/cos 2 A) 1 = tan 2 A Putting the value of cos A = ⅘ (5/4) 2 – 1 = tan 2 A tan 2 A = 9/16 tan A = 3/4Now, using the trigonometric identity 1tan 2 a = sec 2 a sec 2 A = 1 (3/4) 2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4 Example 2 (1 – sin A)/(1 sin A) = (sec A – tan A) 2 Solution Let us take the Left hand side of the equation LHS = (1 – sin A)/(1 sin A)

Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube

Tan^2 identities

Tan^2 identities- It can be concluded that, tan A = 3/4 Now, using the trigonometric identity 1tan2 a = sec2 a sec2 A = 1 (3/4)2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4Substitute the trigonometric identity `tan^2(x) = sec^2(x)1` Note This is the same as `1 tan^2(x) = sec^2(x)` `(tanTo integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 2

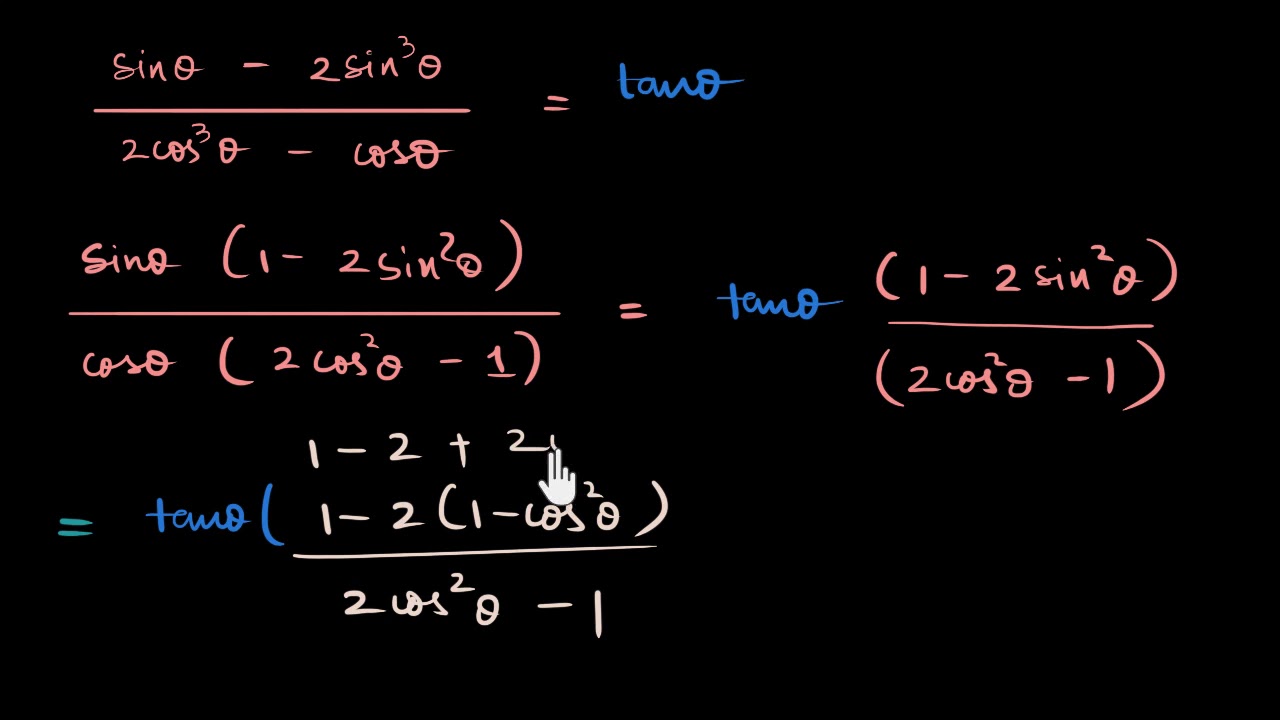
Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

We get (tan(x))2 1 = (sec(x))2 1 = (sec(x))2 (tan(x))2 Now, we will see if 1 = (sec(x))2 (tan(x))2and 1 = (sec(x))2 (tan(x))2 can both be true We can do this by assuming that they are both true, and then add the equations to get 2 = 2(sec(x))2 1=(sec(x))21tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ1 sin 2x = 1 sin 2x (Pythagorean identity) Therefore, 1 sin 2x = 1 sin 2x, is verifiable HalfAngle Identities The alternative form of doubleangle identities are the halfangle identities Sine • To achieve the identity for sine, we start by using a doubleangle identity

In the second method, we used the identity \({\sec}^2 \theta={\tan}^2 \theta1\) and continued to simplify This problem illustrates that there are multiple ways we can verify an identity Employing some creativity can sometimes simplify a procedure As long as the substitutions are correct, the answer will be the sameTrigonometric identities are equations involving the trigonometric functions that are true for every value of the variables involved Some of the most commonly used trigonometric identities are derived from the Pythagorean Theorem , like the following sin 2 ( x) cos 2 ( x) = 1 1 tan 2 Proving the 2nd Pythagorean Identity To prove the 2nd Pythagorean Identity, we start with the 1st Then divide every term by and simplify In the 3rd line take note that is equal to because \ (\tan (x) = \frac {\sin (x)} {\cos (x)\) Also that on the righthandside is equal to because

Trigonometric Identities and Formulas Below are some of the most important definitions, identities and formulas in trigonometry Trigonometric Functions of Acute Angles sin X = opp / hyp = a / c , csc X = hyp / opp = c / a tan X = opp / adj = a / b , cot X = adj / opp = b / a cos X = adj / hyp = b / c , sec X = hyp / adj = c / b ,The key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplified to (a/c) 2 (b/c) 2 = 1Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 p

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

3

71 Solving Trigonometric Equations with Identities;Join this channel to get access to perkshttps//wwwyoutubecom/channel/UCFhqELShDKKPv0JRCDQgFoQ/joinHere is the technique to solve this integration and howReciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos(ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu sec

Trigonometric Identities Youtube

Trigonometric Equations And Identities Trigonometry Math Khan Academy

73 DoubleAngle, HalfAngle, and Reduction Formulas;Identities expressing trig functions in terms of their complements There's not much to these Each of the six trig functions is equal to its cofunction evaluated at the complementary angle Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π Identities for negative anglesDidn't find what you were looking for?

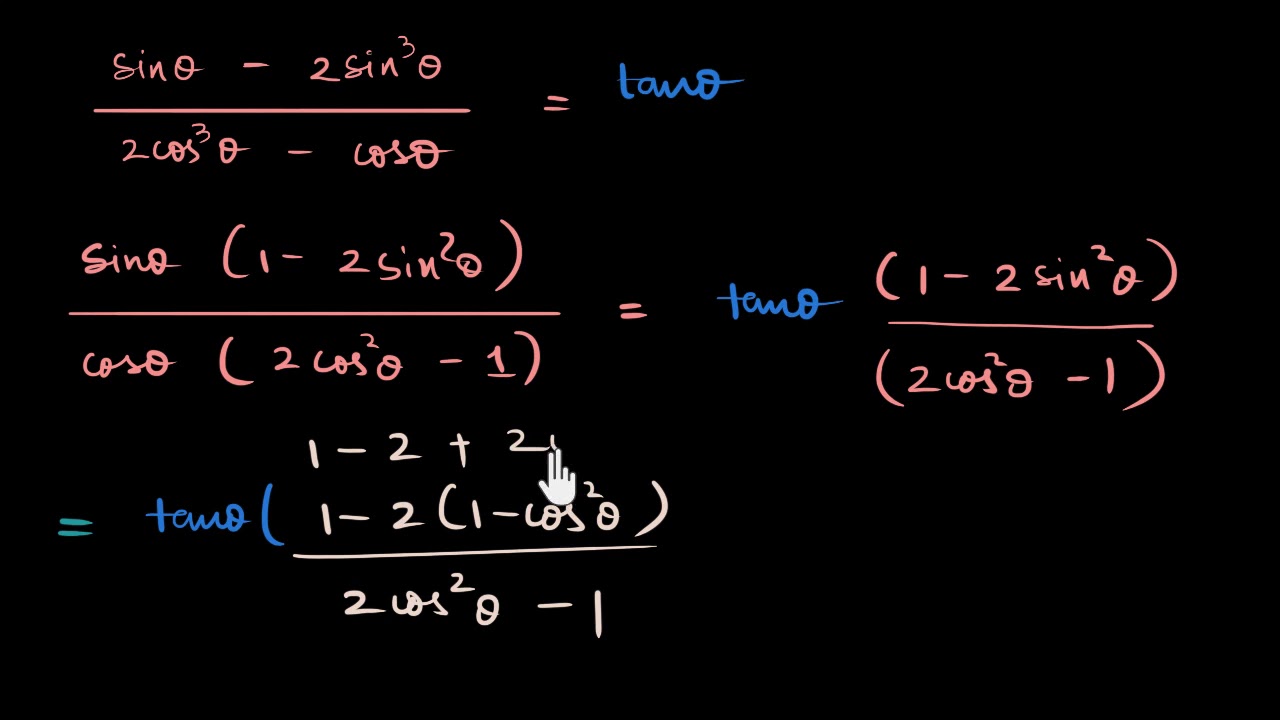
Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy

Http Www Mrsfruge Com Uploads 1 2 0 0 Precalculus Chapter 5 Packet Answers Pdf

Ask for it or check my other videos and playlists!##### PLAYLISTS #####Identities In this unit we are going to look at trigonometric identities and how to use them to solve tan2 A1=sec2 A Thisisanotherimportantidentity Key Point tan2 A1=sec2 A Onceagain,returningto sin 2Acos A =1 wecandividethroughbysin2 A togive sin2 A sin 2A cos2 A sin A = 1 sin2 A But74 SumtoProduct and ProducttoSum Formulas;

2

Solved Find The Remaining Five Trigonometric Functions Of 0 See Example 1 Sin A 0 In Quadrant Ii 32 Cos 0 0 In Quadrant I 33 Tan 0 Course Hero

Trigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum & Difference Identities sin( )=sin cos cos sinTan ⁡ x, cot ⁡ x \tan x, \cot x tanx,cotx is π \pi π Pythagorean identities sin ⁡ 2 A cos ⁡ 2 A = 1 tan ⁡ 2 A 1 = sec ⁡ 2 A cot ⁡ 2 A 1 = csc ⁡ 2 A \begin {aligned} \sin^2 A \cos^2 A &=& 1 \\ \tan^2 A 1 &=& \sec^2 A \\ \cot^2 A 1 &=& \csc^2 A \end {aligned} sin2 Acos2 A tan2 A1 cot2 A1 = = =A trigonometric identity in one variable is an equality that involves trigonometric functions and is true for all values of the variable for which both sides of the equality are defined Recall the Pythagorean theorem that relates the lengths of the sides of a right triangle \{a^2} {b^2} = {c^2},\ where \(a,b\) are the lengths of the triangle's legs and \(c\) is the length of its

Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 262 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Prove the following identities ((1 cot x tan x )(sin x cos x))/(sec^3x cosec^3x) = sin^x cos^2x asked Jun 3 in Trigonometry by Eeshta01 ( 303k points) trigonometric functions

Www Alamo Edu Siteassets Nvc Academics Programs Math Documents 12 Trigonometric Identities Pdf

5 1 5 2 Trigonometric Identities Ppt Download

 Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 175 Solving Trigonometric Equations;The sum identity for tangent is derived as follows To determine the difference identity for tangent, use the fact that tan (−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x

B Prove The Following Trigonometric Identities I Gauthmath

1 1 Csc Or Sin Or Csc Sin 1 Sin Csc X X X X X X 1 1 Sec Or Cos Or

This proves the third powerreducing identity, $\tan^2 \theta = \dfrac{1 – \cos \theta}{1 \cos \theta}$ We've just shown how we can derive the three powerreducing identities using a doubleangle formula It's also possible for us to actually verify this identity using the halfangle identity Let's go ahead and master the threeThe Pythagorean identities are based on the properties of a right triangle cos2θsin2θ =1 1tan2θ =sec2θ 1cot2θ =csc2θ cos 2 θ sin 2 θ = 1 1 tan 2 θ = sec 2 θ 1 cot 2 θ = csc 2 θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angleFor the tangent of the halfangle, tan (2A), we combine the identities for sine and cosine Again replacing A by (1/2)A, we get The following is a summary of the halfangle formulas HalfAngle Identities Sine Cosine Tangent Example Given that sin(A)= 3/5 and 90

Prove The Identity Sec 4 Theta Sec 2 Theta Tan 4 Theta Tan 2 Theta

Trigonometric Identities Solutions Examples Videos

Trigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) en We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The expressions or equations can be possibly simplified by transforming the tan

Http Scibug Com Public Docs Trigonometry Cheat Sheet Pdf

7 Prove One Of The Following Trigonometric Identi Gauthmath

Introduction to Trigonometric Identities and Equations;76 Modeling with Trigonometric EquationsSin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 )

Trig Identities All List Of Trigonometric Identities Learn Trigonometry

Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity

 Trigonometric Identities Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identities mostly refer to Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin ⁡ \sin sin andLet's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ)

Pmt Physicsandmathstutor Com Download Maths A Level C3 Topic Qs Edexcel Set 1 C3 trigonometry trigonometric identities Pdf

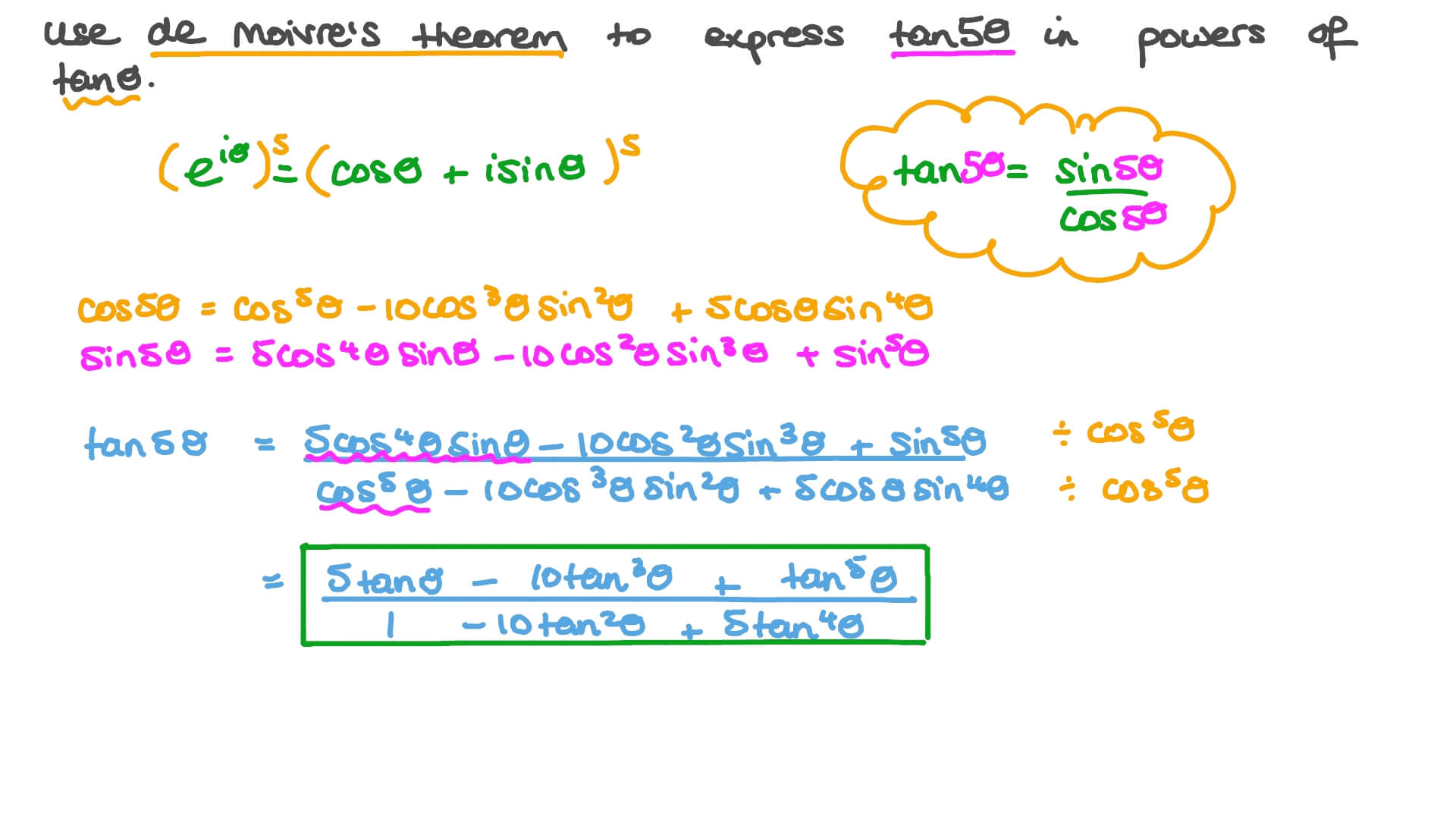
Question Video Using De Moivre S Theorem To Derive Trigonometric Identities Nagwa

Cos 2 ⁡ θ sin 2 ⁡ θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1} The other trigonometric functions can be found along the unit circle as tan ⁡ θ = y B {\displaystyle \tan \theta =y_ {\mathrm {B} }\quad } and cot ⁡ θ = x C , {\displaystyle \quad \cot \theta =x_ {\mathrm {C} },} Well, if we divide (cos(x))2 on both sides;Free Pythagorean identities list Pythagorean identities by request stepbystep This website uses cookies to ensure you get the best experience By

Solved Inquiry 11 8 Marks Prove The Following Trig Iden Chegg Com

Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x

Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x /cos x equation 1 You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3Trigonometricidentitycalculator Prove tan^{2} x * sin^{2} x = tan^{2} x sin^{2} x en

1

Every Day I M Calculatin I D3 Unit Q Pythagorean Identities

Cos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more some other identities (you will learn later) include cos x/sin x = cot x 1 tan^2 x = sec^2 x 1 cot^2 x = csc^2 x hope this helped!72 Sum and Difference Identities;Recall A trigonometric identity is an equation formed by the equivalence of two trigonometric expressions The solution to the equation must be the set of all values of the variable, in which both expressions are defined Examples Example 1 Consider the trigonometric equation

Prove The Following Trigonometric Identities Show Gauthmath

2

Source Trigonometry identities Math Open Reference A Reciprocal identities a1 sin A=1 csc A a4 csc A=1 sin A a2 cos A=1 sec A a5 sec A=1 cos A a3 tan A=1 cot A a6 cot A=1 tan A B Ratio identities b1 tan A= sin A cos A b2 cot A= cos A sin A C

Cofunction Identities In Trigonometry With Proof And Examples Owlcation

Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube

14 1 Trigonometric Identities Ppt Download

Trigonometric Identities Trigonometric Functions Trigonometry

Calc3 1001 By James Bardo Issuu

Cos Sin Tan Csc Sec Cot

Http Www Math Brown Edu Tomg Formulas Pdf

Grade 12 Trigonometry Sum Or Difference Identity Homeworkhelp

Question Video Simplifying Trigonometric Expressions Using Pythagorean Identities Nagwa

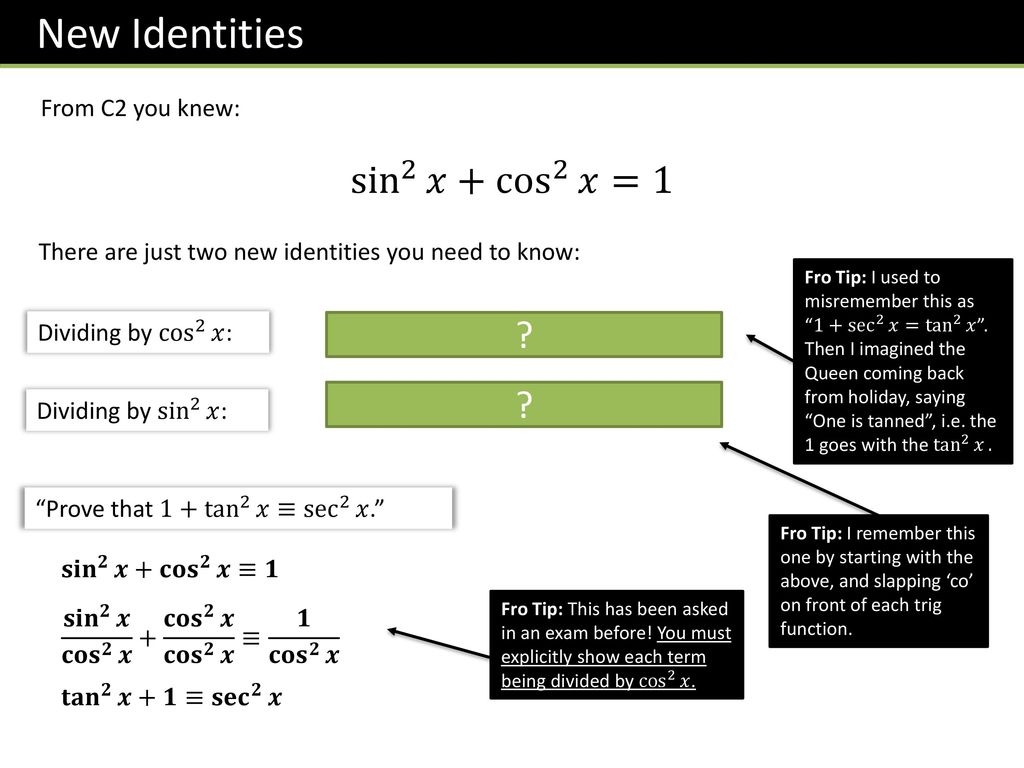
P2 Chapter 6 Trigonometry Ppt Download

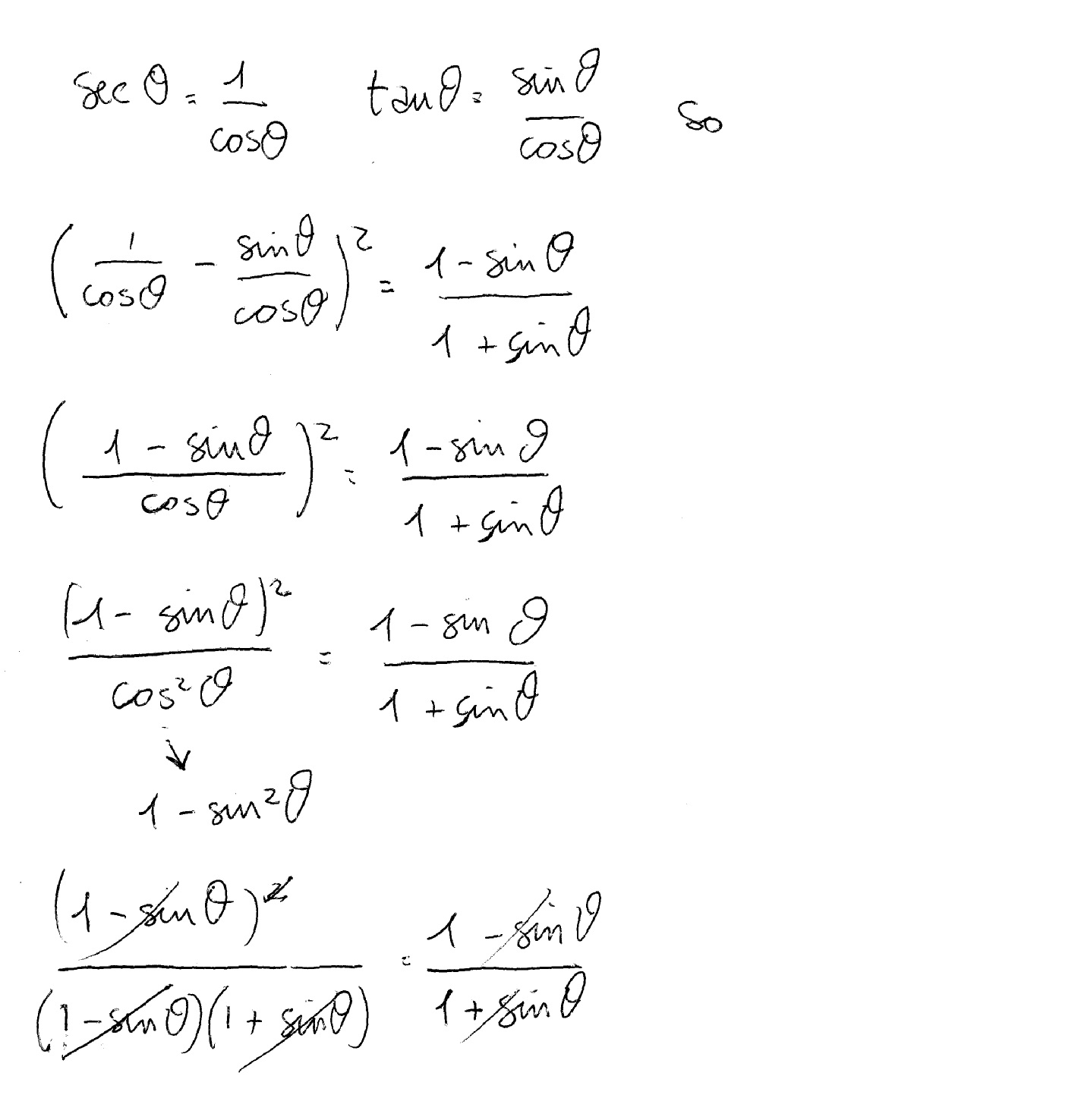
How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Socratic

Www Adelaide Edu Au Mathslearning System Files Media Documents 19 09 Useful Trig Identities Pdf

Cos Sin Tan Csc Sec Cot

Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download

Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 360 th identities packet 16 Pdf

Prove The Following Identities I 4 Marks Each A Gauthmath

Trigonometric Identities

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

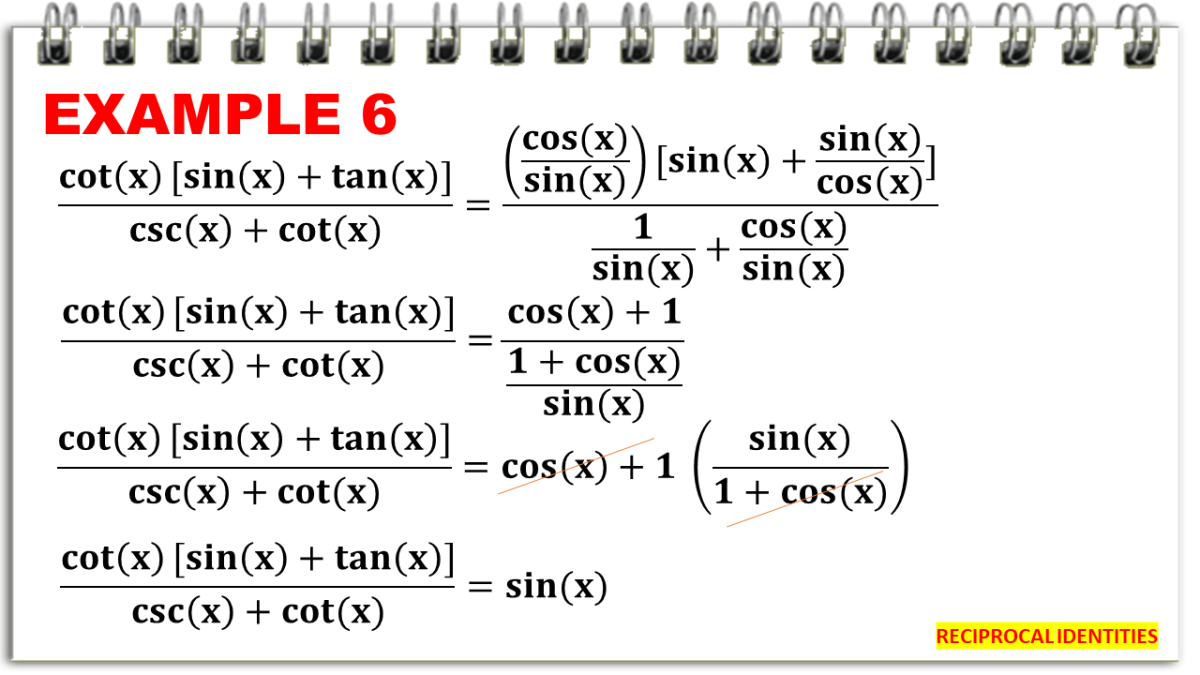
Reciprocal Identities In Trigonometry With Examples Owlcation

Trigonometric Identities Cheat Sheet

Common Identities Properties Of Trigonometric Functions 4 8 Sideway Output To

Stmchs Learning Powerschool Com Rpolicar Introcalculus Cms File Show 2549 Pdf T

Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf

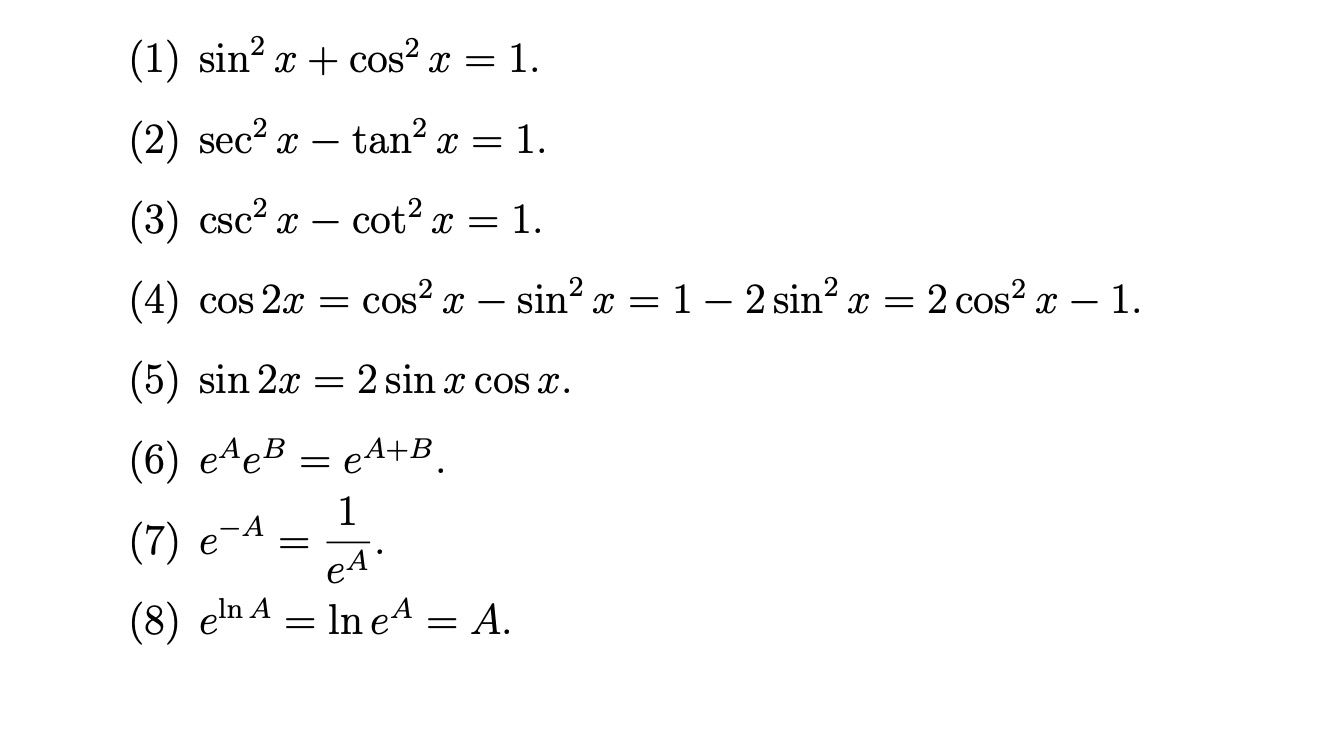
Here Is A List Of Identities Involving Trigonometric Chegg Com

Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf

Www3 Nd Edu Nancy Math Info Trigformulas Pdf

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes

Trigonometric Identities

Trigonometry

Trigonometry Identities English

Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf

Trigonometric Identities A Plus Topper

Ppt 5 1 Fundamental Trig Identities Powerpoint Presentation Free Download Id

Inquiry 11 8 Marks Prove The Following Trig Chegg Com

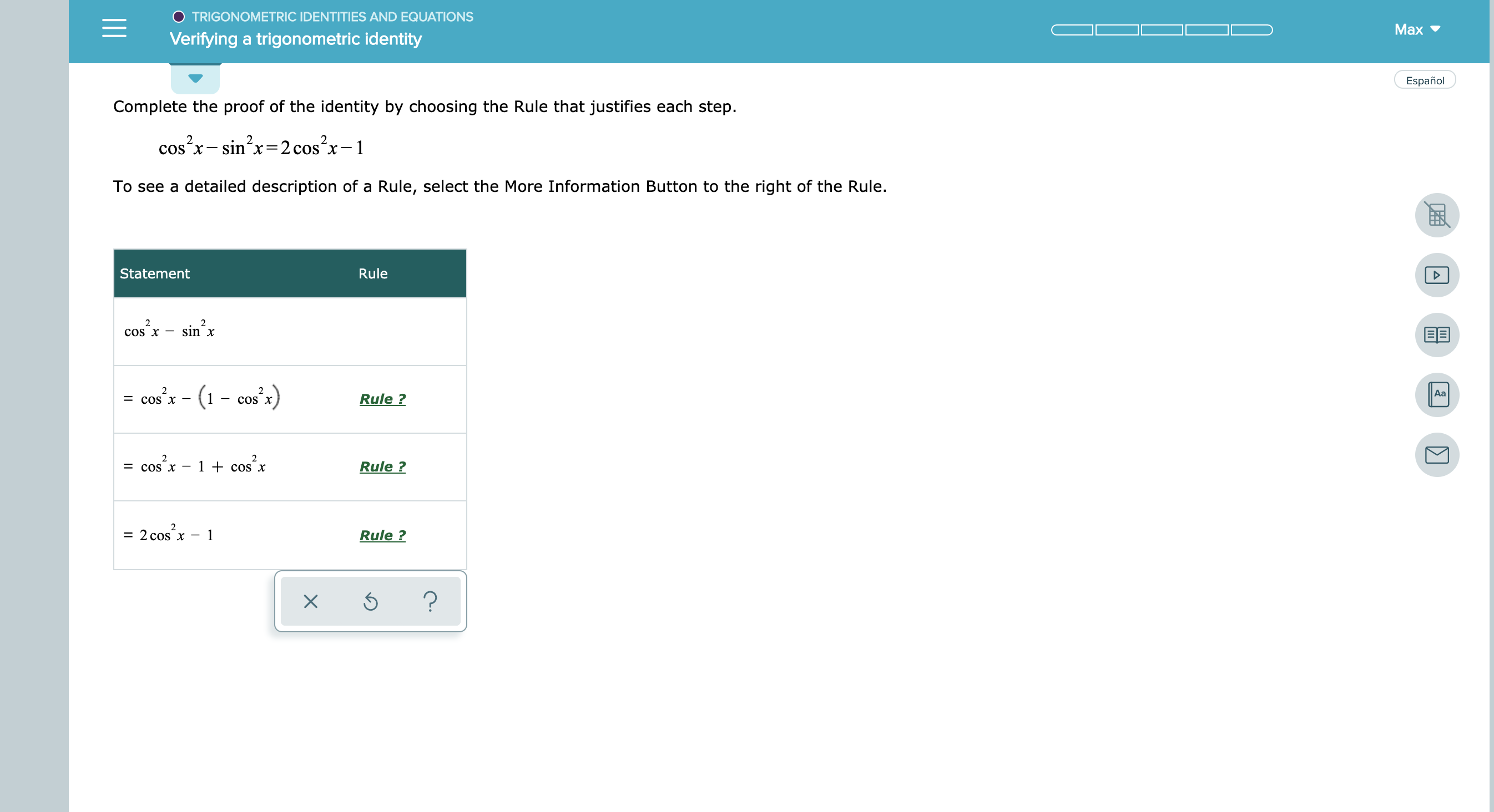
Answered Trigonometric Identities And Equations Bartleby

1

Half Angle Identities

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

Double Angle Formulas What Are Double Angle Formulas Examples

Http Gato Docs Its Txstate Edu Jcr 9ff 4037 48ff 1f A3486fb Trigonometric identities Pdf

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes

Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube

Double Angle Identities Formulas Of Sin Cos Tan Trigonometry Youtube

Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf

The Double Angle Identities Sin2a Cos2a And Tan 2a Derived From The Trigonometric Addition Formulas Hubpages

Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf

Trigonometric Identities

Reciprocal Identities In Trigonometry With Examples Owlcation

Trig Identities Crossword Wordmint

Prove The Following Identities Sin 4 8 Cos 4 8 Gauthmath

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube

Reciprocal Identities In Trigonometry With Examples Owlcation

Ppt Warm Up Powerpoint Presentation Free Download Id

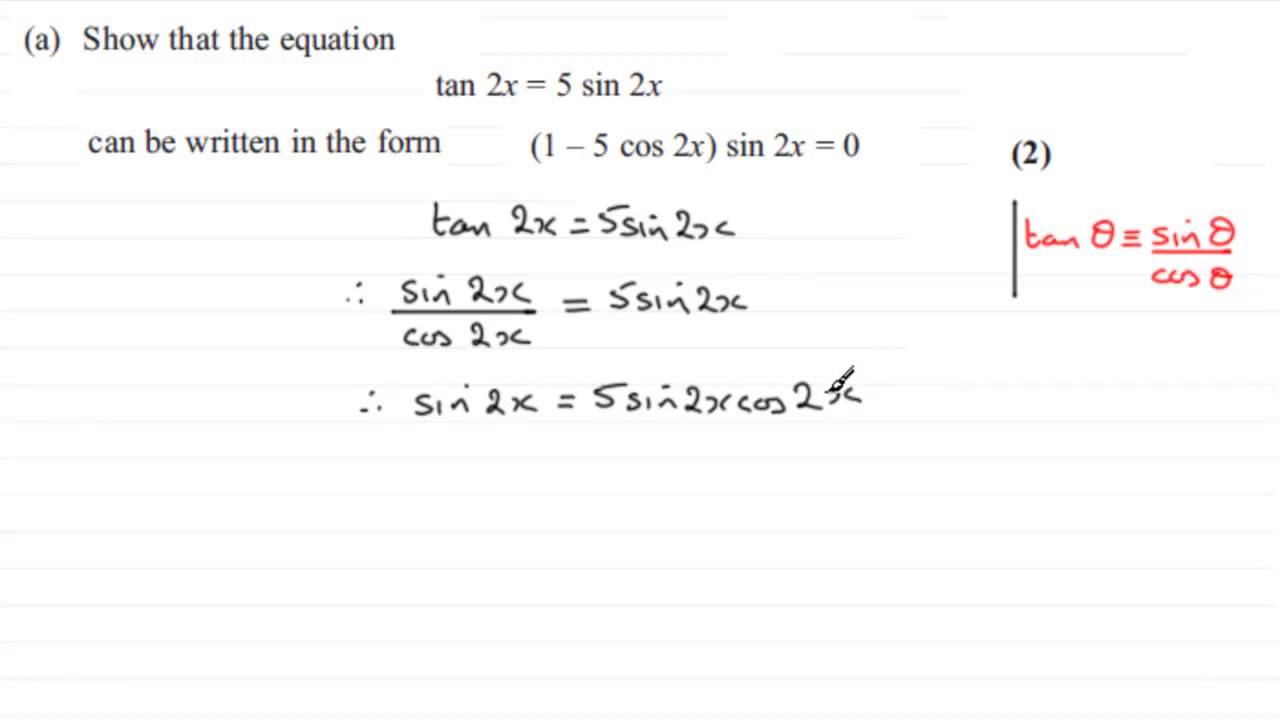
Exam Questions Trigonometric Identities Examsolutions

Trigonometry Reciprocal Identities Expii

Trigonometric Identities Edexcel A Level Maths Pure Revision Notes

How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic

Samantha Douglas Precal 30 Trigonometric Identities Practice Test Answers

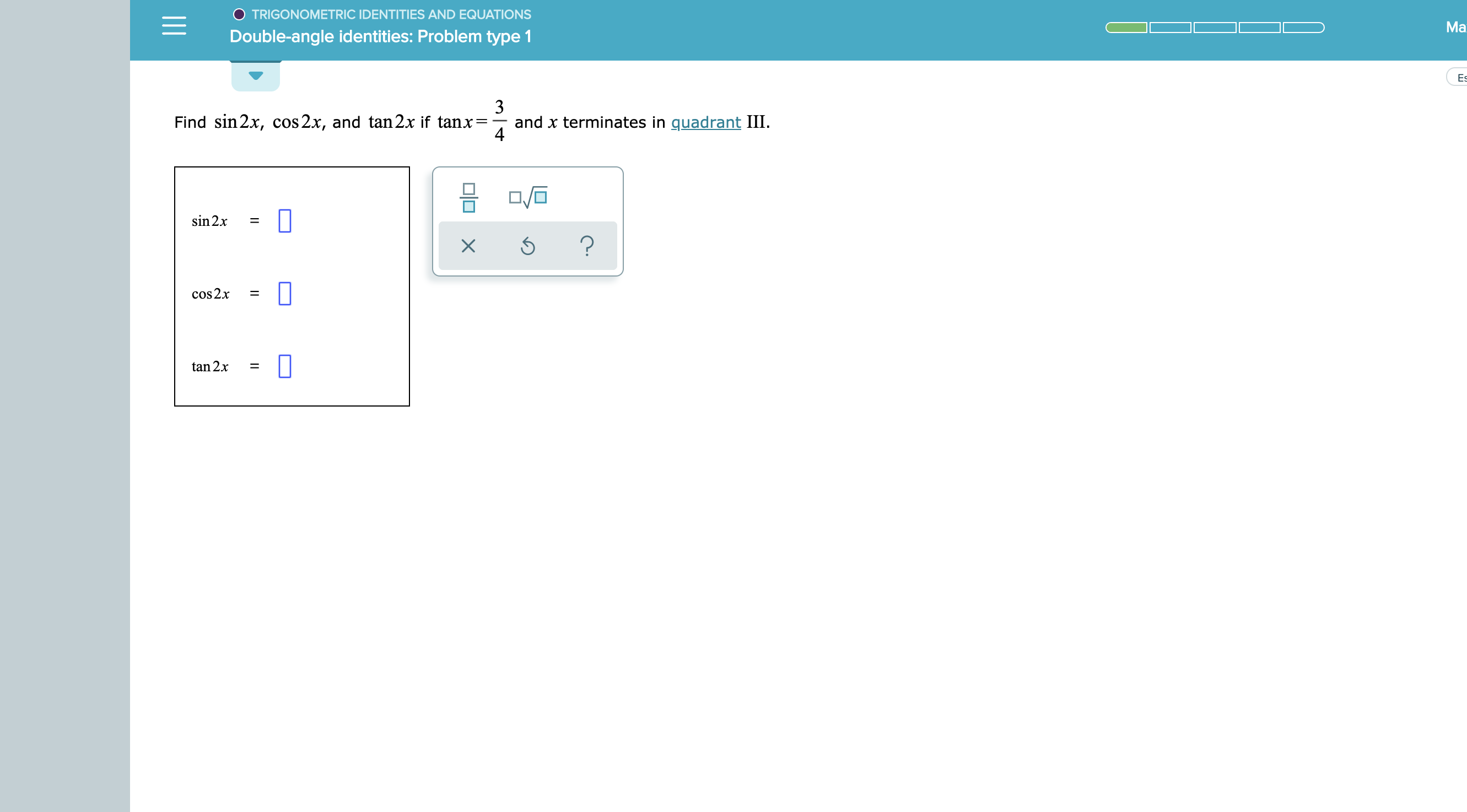
Answered O Trigonometric Identities And Bartleby

3 Simplifying Trig Expression 1 Tan 2x Youtube

Tan 2x Formula What Is Tan 2x Formula Examples

Basictrigonometry Pdf Trigonometric Functions Sine

List Of Trigonometric Identities 2 Docx Document

Trig Identities Study Sheet

Powers Of Trigonometric Functions

10 4 Trigonometric Identities Pdf Free Download

Trig Identities Turn The Wheel

2

Trigonometry Formulas And Identities Full List Teachoo

1

Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf

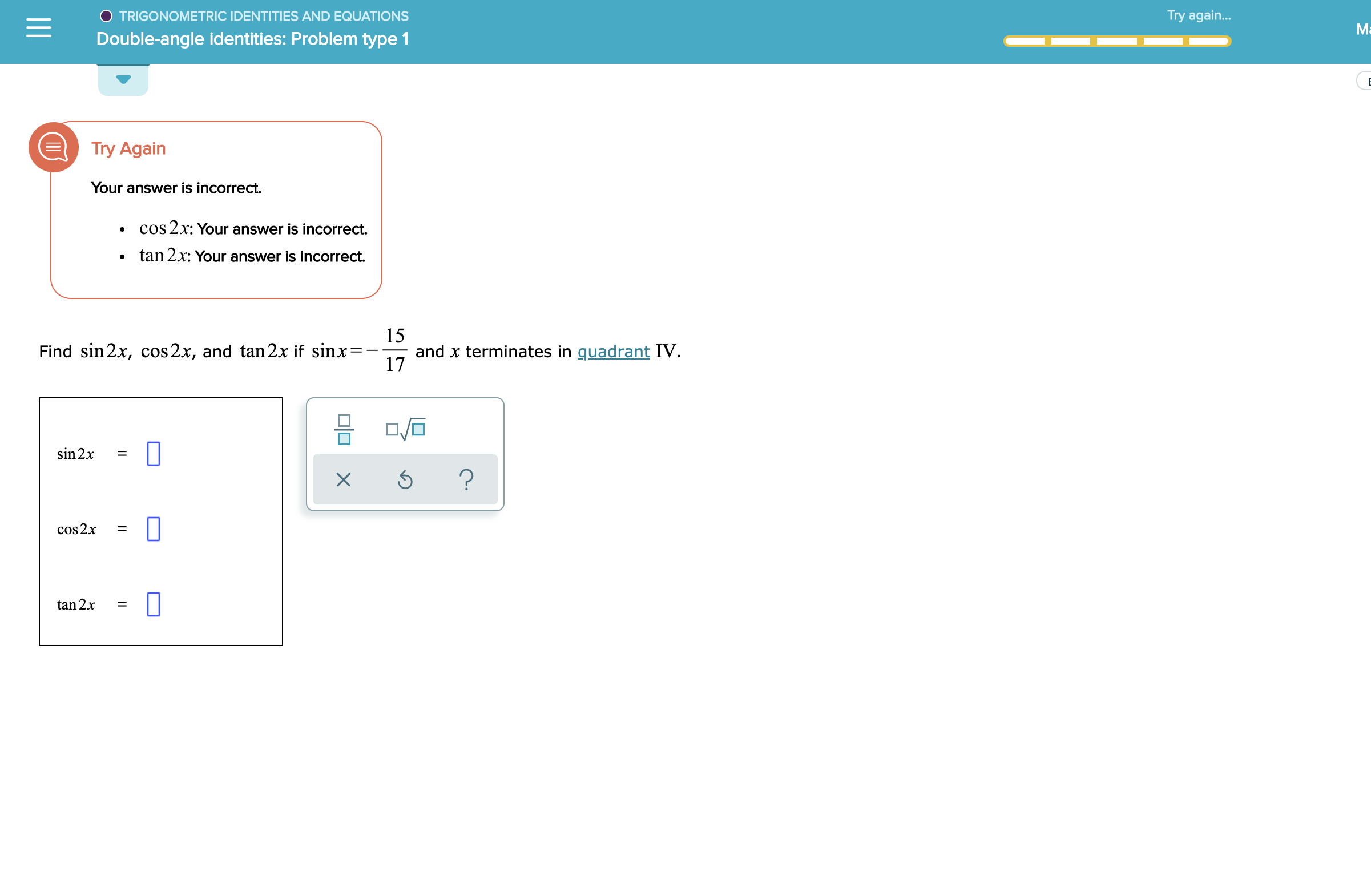
Answered O Trigonometric Identities And Bartleby

How Do You Solve 1 Tan 2x 6 2sec 2x Socratic

Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube

Cos Sin Tan Csc Sec Cot

Incoming Term: tan^2 identities, tan x/2 identities,